gmx msd的进一步探究

前段时间我分享了一个关于气体在炭材料里面扩散的Gromacs模拟的教程，那么众所周知，这个扩散过程肯定就是跟扩散系数是息息相关的，也就是说我们可以进一步的计算气体在材料中的扩散系数来更加准确的描述我们的体系，毕竟这个扩散系数是可以通过实验测量得到的，而计算扩散系数就绕不开均方位移的计算（MSD），gromacs将计算msd的功能集成为gmx msd模块，这个功能非常简单就能学会使用，涉及到的参数并不多，但是不能就被它给欺骗了，实际上有关这个模块的使用还是很复杂的。

多相模拟所遇到的问题

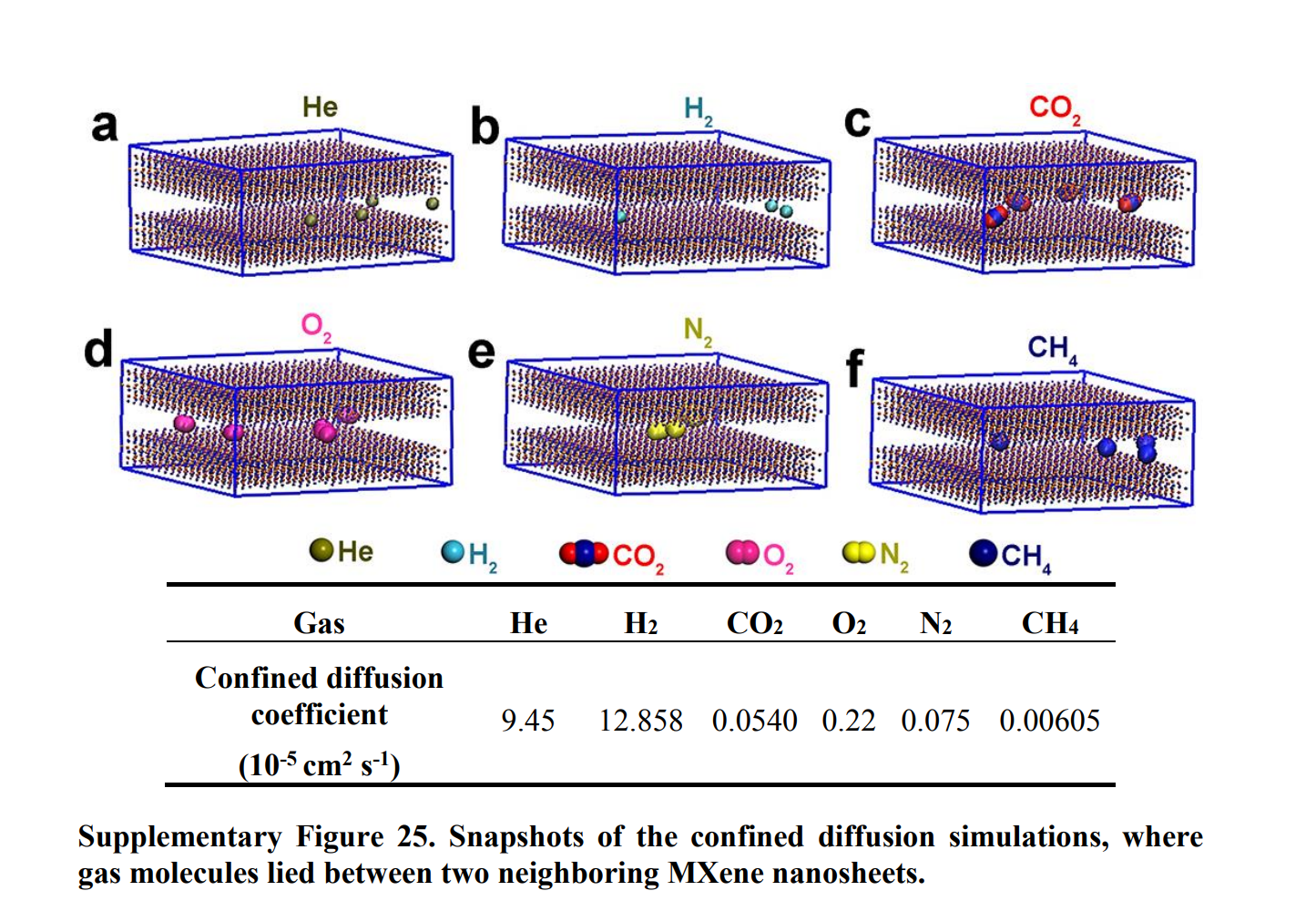
气体在炭材料中的扩散无疑是一个多相的体系，而且我们在模拟的过程中将碳原子固定住了，仅考察气体分子的位移，一定原子数量的炭材料所能负载的气体分子肯定是有限的，所以这个模拟过程中气体分子肯定不能按照实际大气压下同等体积所能包括的气体分子数量进行模拟，我在做这个msd模拟的时候用的是参考文献的结果，文献中在层间嵌入了四个气体分子进行计算，所以我这里是在层间嵌入了五个气体分子进行模拟，我也尝试过更多的气体分子嵌入（30个），但是在模拟的过程中报错。

此外就是关于这个模拟的步长，在进行这样的模拟时是非常容易报错的，大概就是提醒你原子移动的太远，到了一个不合理的位置，然后模拟就崩溃了；这个我在实际计算过程中发现了一些规律，那就是对于大孔径的模型，即层间距比较大的，步长稍微大一点也不会报错，而且当孔径变小，层间距变小，那么再用大的步长就极容易报错，所以如果说是要模拟小孔径下的msd，那么应当尽可能的减小步长，我这里模拟的时候，对于大孔径的材料用的1fs，而对于小孔径的就用的0.5fs，主要是因为我模拟的是氢气，如果是其它相对不活泼的气体的话可以适当增大一倍的步长，但是具体情况还需要自己斟酌。

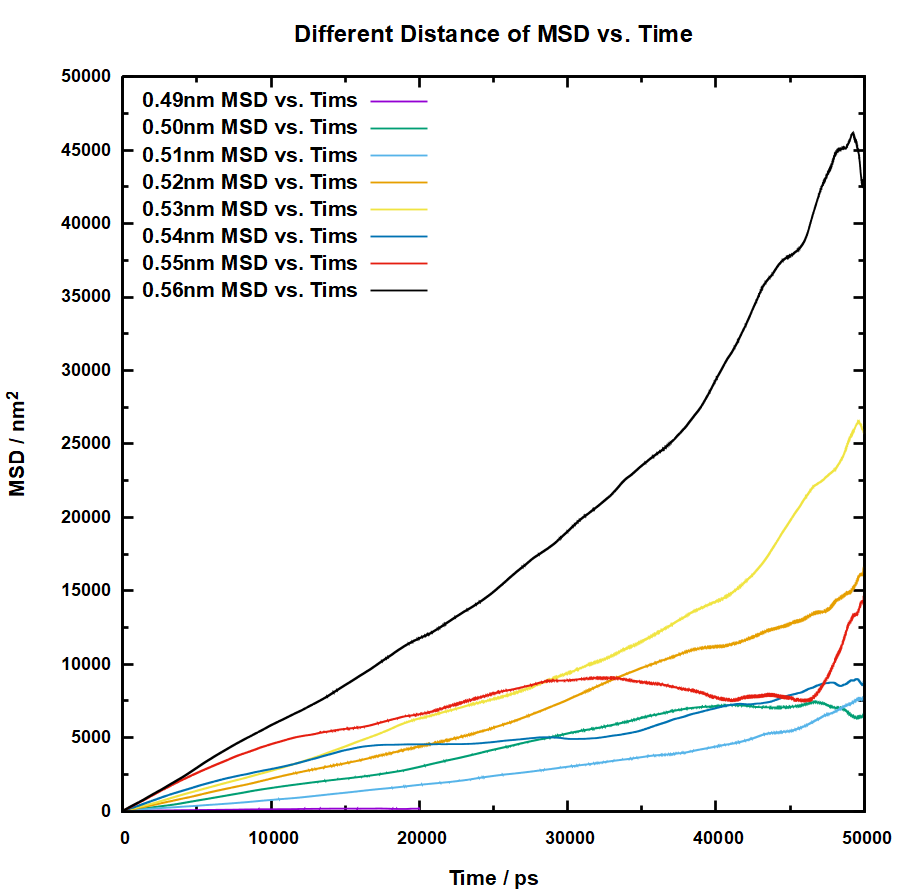
最后也就是我这篇博客所要解决的问题了，那就是msd的模拟以及扩散系数的拟合，在这个模拟的过程中，首要问题是msd曲线是否正常，其次是拟合出来的扩散系数误差是否在能接受的范围内，以下是我得到的不同孔径下的msd曲线：

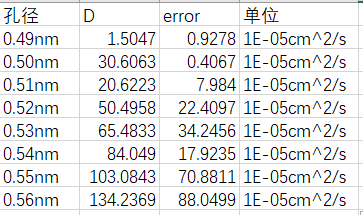
对于0.49nm的孔，由于孔径过小，所以我仅模拟了20ns，可以看出来，0.55nm、0.54nm还有0.50nm的孔在计算msd时有着明显的偏差，的孔径msd曲线也不算正常，那么这个时候我直接用这个数据去计算扩散系数。如下：

这个拟合得到的扩散系数是直接通过gmx msd指令得到的结果，是相当不准确的，134的计算结果误差能有80多，极其的不可靠，因此需要一个新的方法来获取相对可靠的扩散系数。

这里就要感谢gmx群里的樊哲勇老师的细心指导，完全是他一步步指导我到最后得到一个可靠的扩散系数结果的，樊哲勇老师自己也开发了一个开源的分子动力学软件GPUMD，有兴趣的可以了解一下。

gmx msd的分段处理

我此前在模拟的时候陷入了一个误区，就是下意识的任务模拟的时间越长，那么计算的结果就会越准确，一般而言这个认知都是可靠的，但是在计算msd的时候就不行了，或者说没那么准确，这就涉及到一个关联时间的概念，我所理解的关联时间就是计算msd中所用到的模拟时间，而计算msd的关联时间其实不宜太长，虽然通过快速傅里叶变换的计算，gmx可以很轻松的时间计算长达50ns的msd，但是直接用这50ns作为关联时间去计算msd得到的结果就是上面所发的结果，数据是极其不可靠的，所以直接将整个轨迹投入到msd的计算是不行的，要针对具体问题选择合适的关联时间长度的，这就需要对模拟的轨迹进行分段处理，而gmx msd也可以很方便的指定读取的轨迹帧数，也就能很方便的分段处理轨迹。

之前樊老师指导我是将50ns的时间分为了5份，每份10ns来计算msd，而我后面又是计算了一下将轨迹分为50份，每份1ns，但是这样的结果误差相较于5份有一定的增大，这个问题我跟樊哲勇老师请教了一下，他指出可能分为10份这样计算的误差会达到最小，多了的话误差会变大，但是计算出来的平均值应该不会差得太大，所以这个轨迹的分段数量对调整误差大小是有影响的。

由于0.56nm得孔径我之前已经做过了，所以这里我就用0.55nm的孔径来作为演示。

我的模拟过程还是按照之前博客里面写的，按照2步能量最小化，2步预平衡，1步成品模拟的方法来进行模拟的，由于报错的问题，我这里模拟的步长用的是0.5fs，计算完成之后切换到成品模拟的目录下，然后用gmx msd指令计算msd数据。

gmx msd -f 5prd.xtc -s 5prd.tpr -n index.ndx -mol

-n是为了添加索引文件，我在之前模拟的时候就创建了一个index.ndx文件，为了能够指定C原子进行固定，同时也添加了H2的分组，所以这里就可以直接继续使用这个索引文件来选中H2的分组。-mol则是为了计算每个氢气分子的msd，这个指令是直接将整个轨迹都用于计算msd的，也就是50ns，运行一次这个计算的原因是为了验证我后面的方法的确能够减小误差，运行了这个指令之后需要选择组，然后选择氢气的组即可，之后就会输出保存有msd信息的msd.xvg文件以及保存每个氢气的扩散系数信息的diff_mol.xvg文件。

然后就是要开始分段处理了，对于分段可以用如下的指令来指定帧数：

gmx msd -f 5prd.xtc -s 5prd.tpr -n index.ndx -mol -b 0 -e 10000

比如我这里就是选中了模拟开始的0ps处到模拟10000ps的帧来计算msd，对于分成5份来说这样修改5次指令，每次运行结束后将其计算结果导出一下即可，但是为了验证分段对误差的影响，后续我们可能要对轨迹进行数十次的分段，所以这里最好还是写一个脚本，我写的shell脚本如下：

#!/bin/bash

# 指定模拟的全部时长，单位ps
total=50000
# 指定要将轨迹分割的份数
num_parts=5
# 定义输出文件的目录
dir_name=1test

# 计算每一份轨迹的时长
part_size=$((total / num_parts))

# 定义开始的帧数，从第0帧开始
begin_time=0

# 定义一份轨迹的结尾的时长，
end_time=$part_size

# 遍历所有份数，依次处理
for ((i = 0; i < num_parts; i++)); do
    echo "Processing range $begin_time - $end_time"

# 执行gmx msd指令，将分割的轨迹依次传递给gmx执行，eof后面的4是因为氢气分组的编号为4
gmx msd -f 5prd.xtc -s 5prd.tpr -n index.ndx -mol -b $begin_time -e $end_time << EOF
4

EOF
    # 保存文件
    mv msd.xvg ./$dir_name/${end_time}msd.xvg
    mv diff_mol.xvg ./$dir_name/${end_time}mol.xvg
    
    # 更新开始时间和结束时间
    begin_time=$end_time
    end_time=$((end_time + part_size))
done

这个脚本是我自己写的，可以根据模拟时长来自动按照需要的分段数量进行分割，其中执行gmx msd的指令那一部分，对于EOF里面的内容是需要根据自己要对哪个组进行msd计算来修改的，我msd计算的时候氢气是第四组，所以这里是4，然后空一行代表对选中4这个组的确定。文件输出到的目录是需要在工作目录下自己创建一个文件的，比如我自己创建一个叫做1test文件来存储将轨迹分为5部分的msd文件，那么我就要将dir_name这个变量定义，为了验证猜想，我决定依次分割为5、10、25、50份轨迹来分别计算最后得到的扩散系数的值以及误差。

将上面的代码保存为cal_msd.sh文件，然后创建四个文件来保存输出的文件，注意要提前保留未分割轨迹时输出的msd文件。

mkdir 1test 2test 3test 4test
sh cal_msd.sh

然后每次运行前修改一下cal_msd.sh的文件内容，主要修改轨迹分割的份数以及文件输出的目录。

绘制msd曲线并计算平均msd

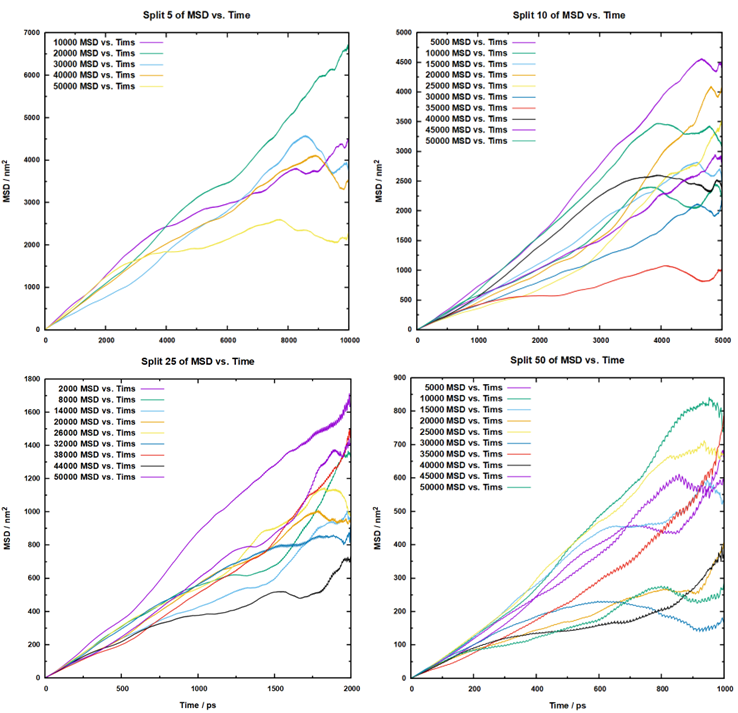
将所有分割的轨迹msd计算完毕之后，就可以开始绘图了，对于25份和50份的没办法全部拿出来，所以我抽样了部分数据画在图上，如下：

我这里是用的gnuplot来绘图，以分割五份的绘图为例，代码如下：

set terminal wxt font "Arial Bold,7" size 500,500 

#set multiplot layout 3,3

file1 = "10000msd.xvg"
file2 = "20000msd.xvg"
file3 = "30000msd.xvg"
file4 = "40000msd.xvg"
file5 = "50000msd.xvg"

set title font "Arial Bold,8"  # 设置标题字体和字体大小
set xlabel font "Arial Bold,7"  # 设置x轴标签字体和字体大小
set ylabel font "Arial Bold,7"  # 设置y轴标签字体和字体大小
set xtics font "Arial Bold,6"  # 开启小刻度  设置x轴刻度字体和字体大小
set ytics font "Arial Bold,6"  # 设置y轴刻度字体和字体大小
set mxtics 2
set mytics 2

set style line 1 lt 1 lw 2  # 设置曲线样式为实线、宽度为2
set border lw 1.5  # 设置边框宽度为1.5

set xlabel "Time / ps"  # 设置x轴标签
set ylabel "MSD / nm\^2"  # 设置y轴标签

set key left top # 将图例放在左上角

set title "Split 5 of MSD vs. Time"  # 设置图形标题
plot file1 using 1:2 with lines title "10000 MSD vs. Tims",\
     file2 using 1:2 with lines title "20000 MSD vs. Tims",\
     file3 using 1:2 with lines title "30000 MSD vs. Tims",\
     file4 using 1:2 with lines title "40000 MSD vs. Tims",\
     file5 using 1:2 with lines title "50000 MSD vs. Tims",\

根据上面的图可以看出来，误差还是挺大的。所以接下来要进一步处理，就是计算所有点的平均值以及标准误差，还是以分割五份的距离，这50ns的数据我们都不想放弃，那么肯定要参考它的平均值，那么就是对每个横坐标下的msd值进行求平均，这样我们可以得到一个0-10000ps的平均msd曲线，这意味着我们要对这五个文件进行处处理，而且是对每个文件里的每个点都要拿出来进行求和平均，Excel可以做到这一点，但是有亿点点麻烦，所以这里就需要用到万能的python了，我写了一个脚本，它可以自动读取当前目录下的msd.xvg结尾的文件，然后从第21行开始读取数据，再对第二列数据进行加和，并根据文件数来进行平均并计算标准误差，代码如下：

import glob
import numpy as np

def error_cal(time_step):
    # 指定文件的描述符
    pattern = r'*msd.xvg'
    # 获取所有文件的路径
    file_names = glob.glob(pattern)
    #print(len(file_names))
    data_list = []

    # 遍历读取文件内容
    for file_name in file_names:
        # print(file_name)
        with open(file_name, 'r') as file:
            # 读取文件，从第21行读取，跳过前面的非数据内容
            lines = file.readlines()[20:]
            columns = []
            for line in lines:
                # 清洗数据并将第二列的数据提取出来
                column_split = line.strip().split()[1]
                columns.append(column_split)
            # 将所有MSD数据打包进一个列表之后，将这个列表再存入总的列表中
            data_list.append(columns)

    # 确定msd点的数量
    msd_dots = len(data_list[0])

    # 存储所有文件里面每个时间点MSD的信息的列表，整合
    result_list = []

    # 存储计算得到的平均MSD以及误差等信息的列表
    final_list = []
    #依次读取同一个位置下的MSD数据
    for j in range(0, msd_dots):
        temp_list = []
        for i in range(0, len(file_names)):
            temp_list.append(float(data_list[i][j]))
        # print(temp_list)
        result_list.append(temp_list)
        
        # 用numpy计算平均值与标准误差
        mean_value = np.mean(temp_list)
        std_error = np.std(temp_list, ddof=1) / np.sqrt(len(temp_list))
        
        # 将计算得到的数据存入列表
        final_list.append([j * time_step, mean_value, std_error])
    
    # 设定输出的文件信息格式
    data_str = '\n'.join(' '.join(map(str, sublist)) for sublist in final_list)
    
    # 将计算得到的数据输出未cal.xvg
    with open('cal.xvg', 'w') as file:
        file.write(data_str)
    return result_list

def main():
    # 设定步长，单位ps
    time_step = 2
    result_list = error_cal(time_step)
 
if __name__ == '__main__':
    main()
print("hello world")

这个python脚本执行后就会产生一个cal.xvg文件，里面第一列是时间坐标，也就是按照时间步长来增长的值，注意，在运行的时候定义的time_step并不是mdp文件里面的步长，它是你记录的轨迹的时间步长，所以它的值应该是你的mdp文件里面dt*nstxout-compressed的值，比如我这里模拟的时候设置的步长为1fs，也就是0.001ps，然后2000步记录一次轨迹，那么就是2ps。然后文件的第二列就是平均的msd，第三列就是标准误差，标准误差我是用的numpy库里面的函数计算的，自由度为n-1。

这样我们可以将这个平均数据附带误差棒的图绘制出来，可以直接绘制在之前的图上，为了方便区分，我将之前的数据线更改为了虚线，gnuplot的代码如下：

set terminal wxt font "Arial Bold,7" size 500,500 

#set multiplot layout 3,3

file1 = "10000msd.xvg"
file2 = "20000msd.xvg"
file3 = "30000msd.xvg"
file4 = "40000msd.xvg"
file5 = "50000msd.xvg"
file6 = "cal.xvg"


set title font "Arial Bold,8"  # 设置标题字体和字体大小
set xlabel font "Arial Bold,7"  # 设置x轴标签字体和字体大小
set ylabel font "Arial Bold,7"  # 设置y轴标签字体和字体大小
set xtics font "Arial Bold,6"  # 开启小刻度  设置x轴刻度字体和字体大小
set ytics font "Arial Bold,6"  # 设置y轴刻度字体和字体大小
set mxtics 2
set mytics 2

set style line 1 lt 1 lw 2  # 设置曲线样式为实线、宽度为2
set style line 2 lc rgb 'light-blue' lt 1 lw 1.5  # 设置曲线样式为实线、宽度为0.5
set border lw 1.5  # 设置边框宽度为1.5

set xlabel "Time / ps"  # 设置x轴标签
set ylabel "MSD / nm\^2"  # 设置y轴标签

set key left top # 将图例放在左上角

set title "Split 5 of MSD vs. Time"  # 设置图形标题
plot file6 using 1:2:3 with errorbars ls 2 title "errorbars of mean MSD",\
     file6 using 1:2 with lines title "mean MSD vs. Times",\
     file1 using 1:2 with lines dt 2 title "10000 MSD vs. Tims",\
     file2 using 1:2 with lines dt 2 title "20000 MSD vs. Tims",\
     file3 using 1:2 with lines dt 2 title "30000 MSD vs. Tims",\
     file4 using 1:2 with lines dt 2 title "40000 MSD vs. Tims",\
     file5 using 1:2 with lines dt 2 title "50000 MSD vs. Tims",\

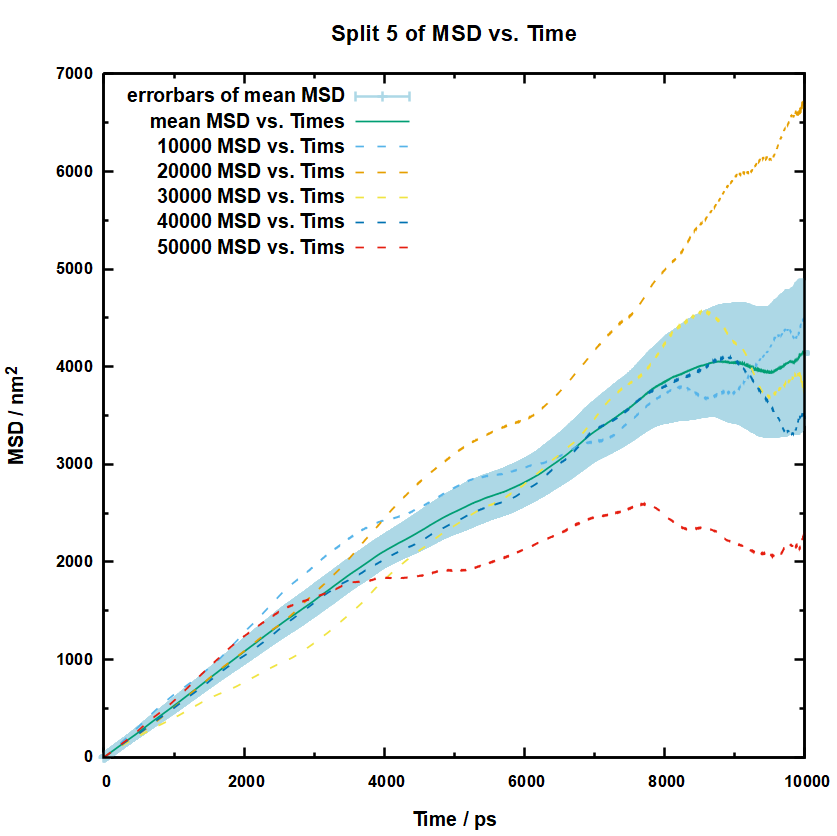
用上面的代码绘制出来的图片如下：

计算扩散系数以及误差

可以看到随着关联时间的增大，误差是愈发的大的，然后所以这里可以着眼于初始的那数百ps的结果，为了更加明显的关注这些信息，可以在gnuplot的代码里面添加这行指令：

set xrange [0:1000]

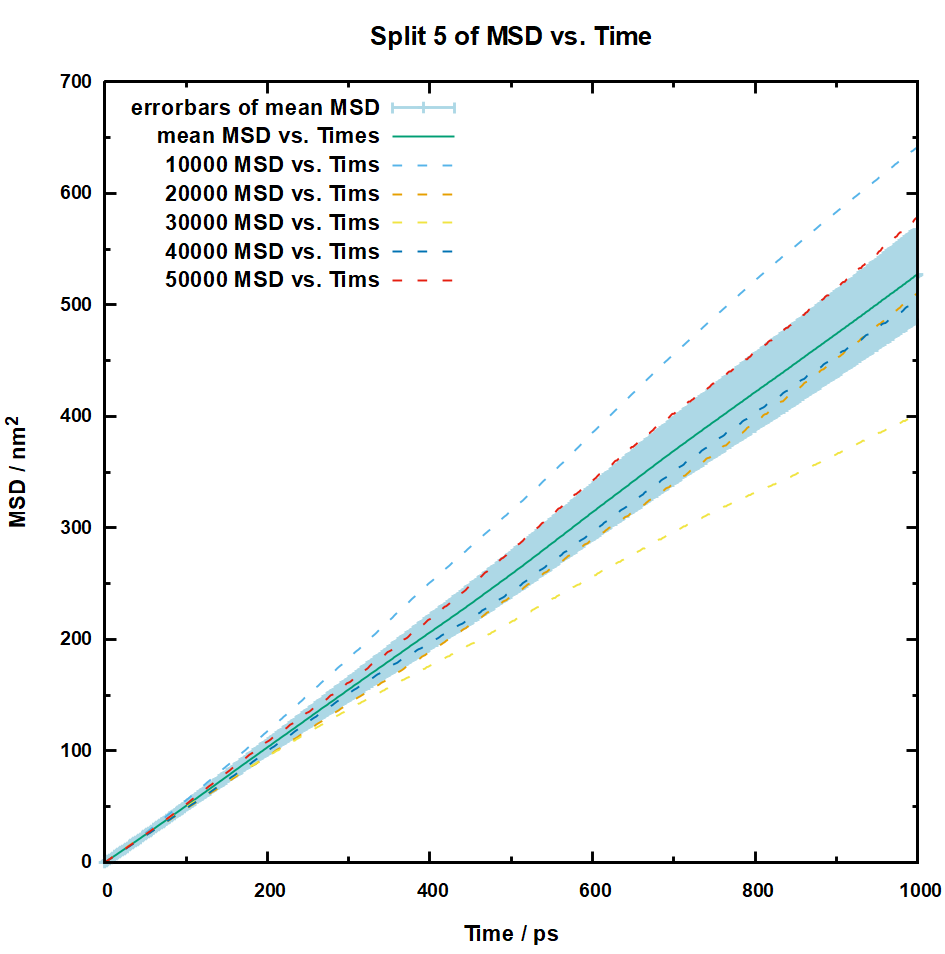
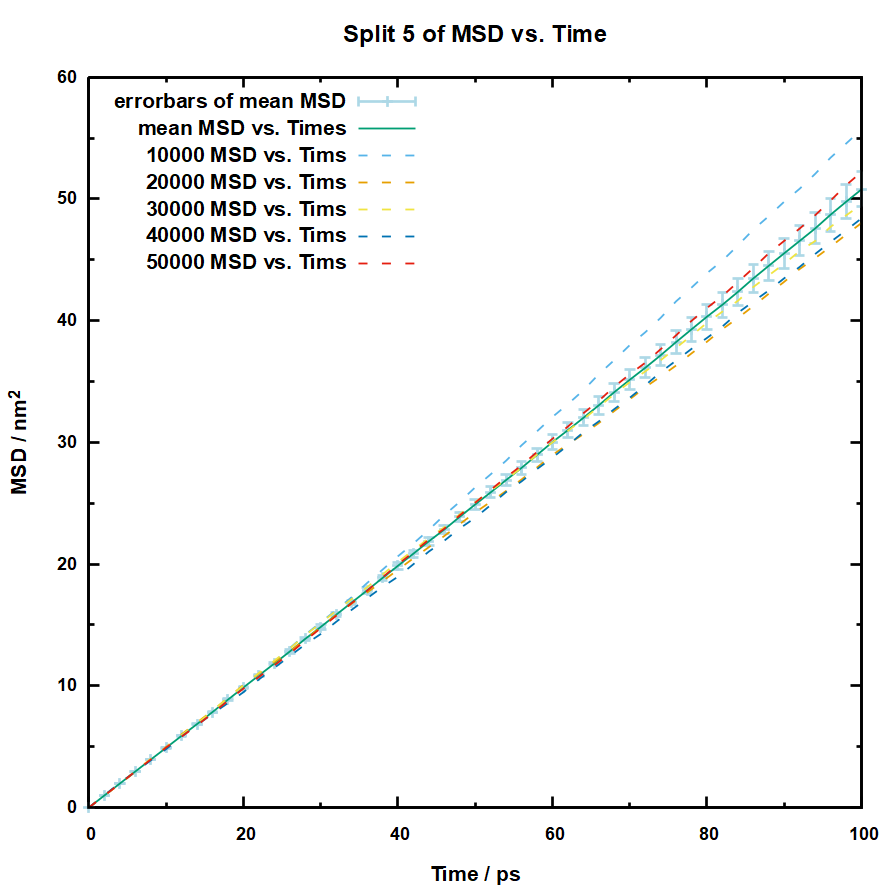
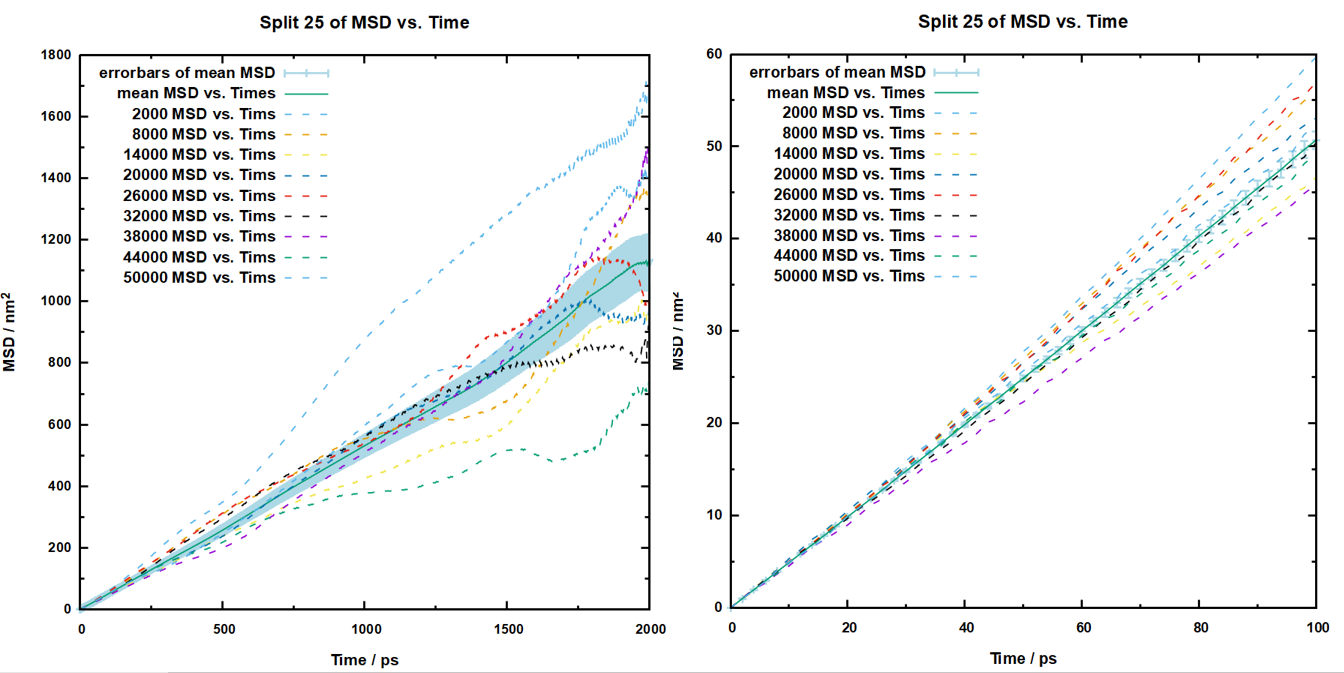
以下是我在gnuplot的代码里面分别通过set xrange指定0-1000和0-100ps绘制的结果：

可以看到1000ps的误差可能还是比较大，但是在100ps的时候误差就已经在可以接受的范围内了，所以我们可以直接用这个100ps的数据去拟合扩散系数，拟合的方法也很简单，直接将每个分割出来的轨迹提取第100ps的msd，然后用爱因斯坦方程：

$$D = MSD/6t$$

即可求得扩散系数，这样我们分割五份轨迹就可以得到5个扩散系数，然后求平均值，再求标准误差即可，这个我们也可以很方便的通过python实现，我们可以直接在之前的代码上添加，添加相关代码的完整内容如下：

import glob
import numpy as np

def error_cal(time_step):
    # 指定文件的描述符
    pattern = r'*msd.xvg'
    # 获取所有文件的路径
    file_names = glob.glob(pattern)
    #print(len(file_names))
    data_list = []

    # 遍历读取文件内容
    for file_name in file_names:
        # print(file_name)
        with open(file_name, 'r') as file:
            # 读取文件，从第21行读取，跳过前面的非数据内容
            lines = file.readlines()[20:]
            columns = []
            for line in lines:
                # 清洗数据并将第二列的数据提取出来
                column_split = line.strip().split()[1]
                columns.append(column_split)
            # 将所有MSD数据打包进一个列表之后，将这个列表再存入总的列表中
            data_list.append(columns)

    # 确定msd点的输了
    msd_dots = len(data_list[0])

    # 存储所有文件里面每个时间点MSD的信息的列表，整合
    result_list = []

    # 存储计算得到的平均MSD以及误差等信息的列表
    final_list = []
    #依次读取同一个位置下的MSD数据
    for j in range(0, msd_dots):
        temp_list = []
        for i in range(0, len(file_names)):
            temp_list.append(float(data_list[i][j]))
        # print(temp_list)
        result_list.append(temp_list)
        mean_value = np.mean(temp_list)
        std_error = np.std(temp_list, ddof=1) / np.sqrt(len(temp_list))
        final_list.append([j * time_step, mean_value, std_error])

    data_str = '\n'.join(' '.join(map(str, sublist)) for sublist in final_list)
    with open('cal.xvg', 'w') as file:
        file.write(data_str)
    return result_list


def d_coef_cal(result_list, time_step, time_set):
    d_coef_list = []
    # 遍历指定时间点下的所有msd数据，并将其存入列表
    for i in result_list[int(time_set / time_step)]:
        # 计算扩散系数，*1000为转化单位为1E-05cm^2/s
        d_coef = i / 6 / time_set * 1000
        d_coef_list.append(d_coef)

    # 计算平均值和标准误差
    mean_value = np.mean(d_coef_list)
    std_error = np.std(d_coef_list, ddof=1) / np.sqrt(len(d_coef_list))

    # 打印相关信息
    # print("扩散系数列表为：", d_coef_list)
    print("平均扩散系数为：" + str(mean_value))
    print("标准误差为：+/- " + str(std_error))

def main():
    # 设定步长，单位fs
    time_step = 2
    result_list = error_cal(time_step)

    # 设定求扩散系数的时间点
    time_set = 100
    d_coef_cal(result_list, time_step, time_set)

if __name__ == '__main__':
    main()
print("hello world")

我就是在之前的基础上添加了一个d_coef_cal的函数，用它来读取我们之前已经获取到的有关msd的列表，然后提取第100ps的msd进行求和平均以及计算误差等操作，最后将其打印出来，这里的时间点是需要我们自行在文件里面进行修改的，设定好时间点之后就可以直接运行这个小脚本，然后我们就可以获得以当前目录下所有msd.xvg文件计算得到的一个平均扩散系数，最后的hello world可以忽略。。

平均扩散系数为：84.63489999999999
标准误差为：+/- 2.388606642073061
hello world

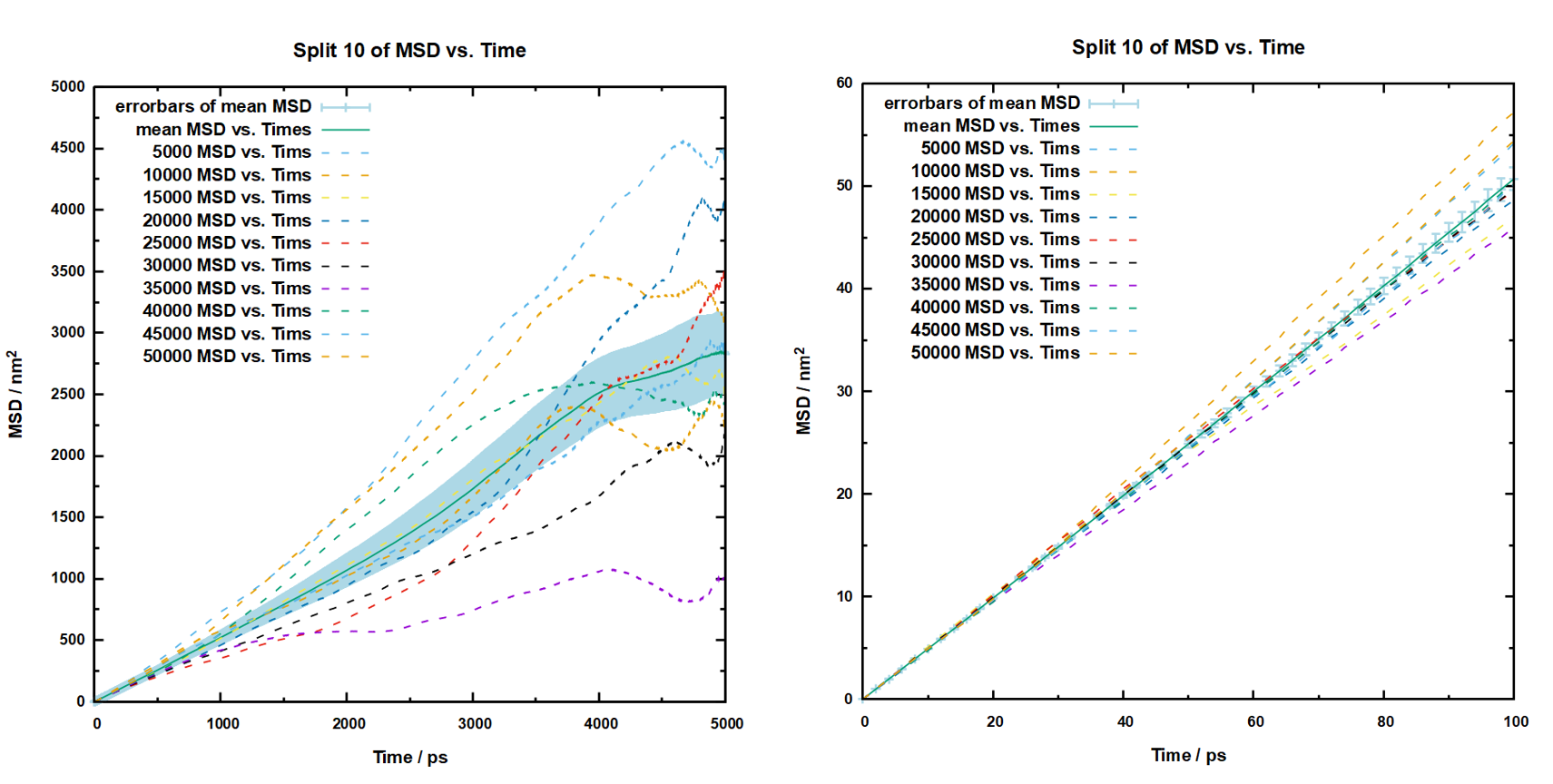
以上就是我的计算结果，最终误差+/-2.4左右，扩散系数为84.635*1E-05cm^2/s。这样我们就完成了分割五份的情况下的扩散系数的计算，一般来说这样就已经可以了，接近3%的误差是在可以接受的范围内的，但是我们为了探寻一下切割份数对计算结果的影响，就可以继续对其它数据进行处理，不过根据这一部分的工作，对其它轨迹分割的数据处理是相当的快速了，此前我们已经通过cal_msd.sh文件将分割10份、25份以及50份的文件分别保存了下来，并且也绘制了相关的图，那么我们可以将它们的平均msd以及带误差棒的数据绘制出来，然后也仅截取0-100ps的数据查看：

对于分割为10份的msd计算，最终得到的扩散系数以及误差如下：

平均扩散系数为：84.50768333333335
标准误差为：+/- 1.8481349505216076
hello world

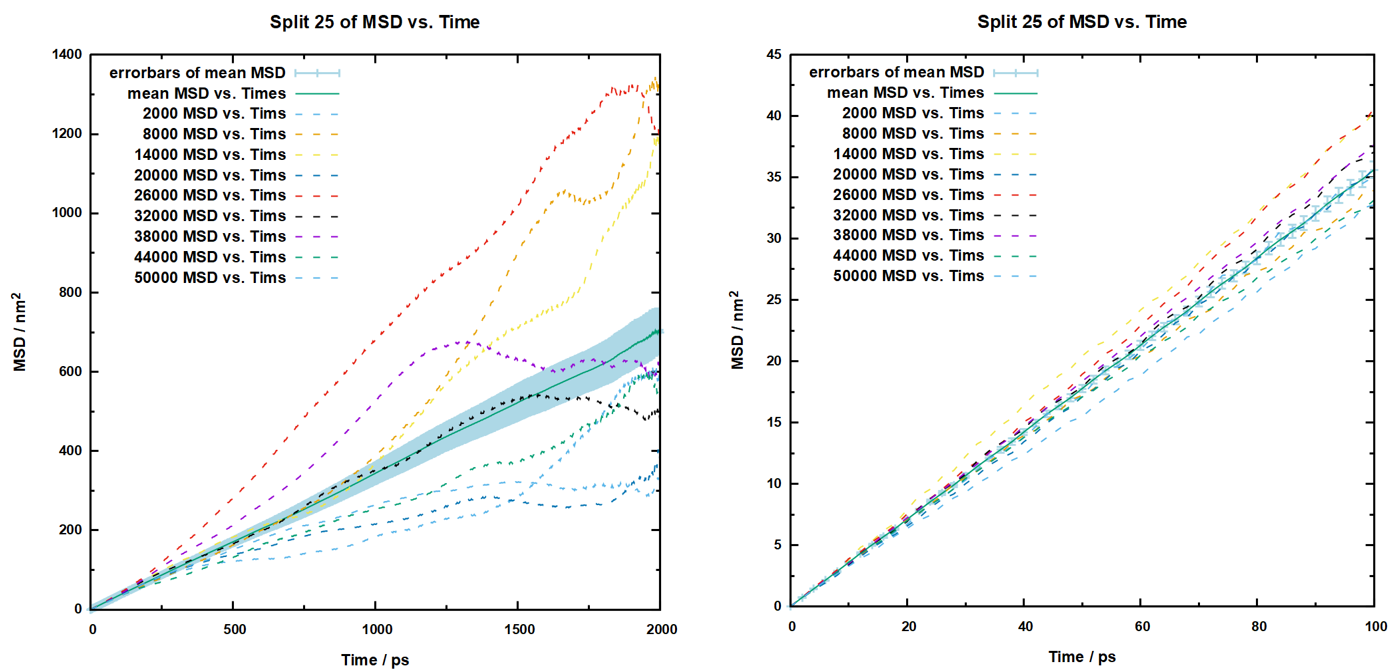
然后是轨迹分割为25份的数据处理，绘图如下：

然后计算的到的扩散系数以及误差如下：

平均扩散系数为：84.46822
标准误差为：+/- 1.5590761242705153
hello world

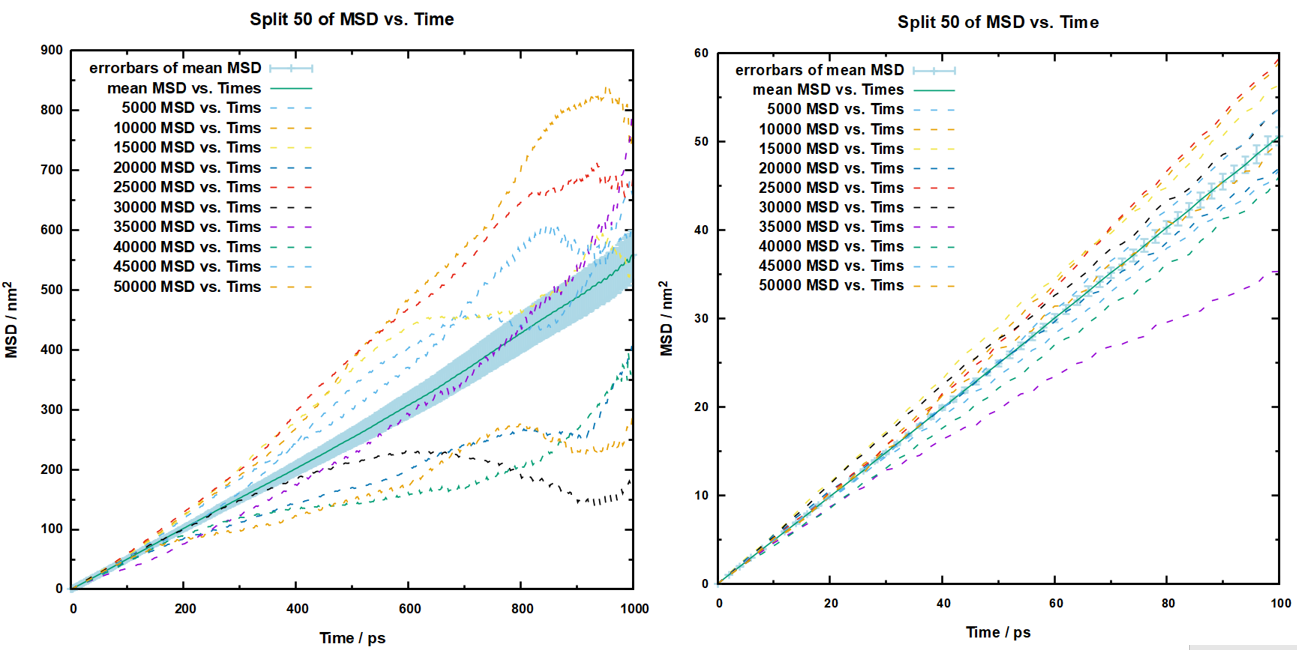
最后是轨迹分割为50份的数据处理，绘图如下：

然后计算的到的扩散系数以及误差如下：

平均扩散系数为：84.33105000000002
标准误差为：+/- 1.7107163494188433
hello world

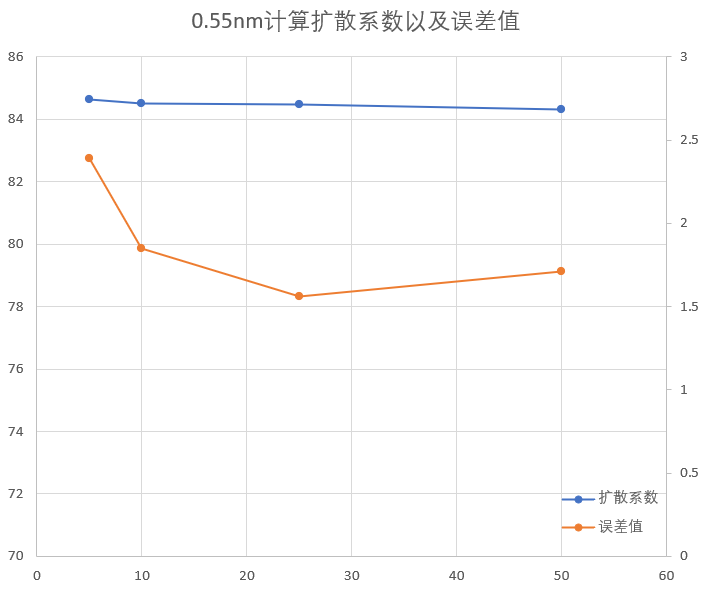
这样处理完之后将所有数据整合一下，再绘制一个图，如下：

可以看出来，这样计算出来的扩散系数差异不大，而误差值的差异则与分割的份数有关，有一个最佳的分割份数，具体是多少不好说，但是应该是介于25-50份之间。而反观最初的0.55nm计算的扩散系数的结果为104+/-70，我们在这其中随意选中一个数据都是相当可靠的计算结果了。

最后采用的msd计算方法

根据前面的探讨，我们基本可以暂时认为将轨迹分割为25份是一个最佳的处理方法，那么就可以以这样的方法去处理其它数据，为了防止读者看了前面的探究过程，有点不太懂，而我也要继续处理后面的数据，那么我就想再以0.54nm为例，用最佳的分割25份的方法处理一下数据。

切换到0.54nm成品模拟的目录下，将前面我们的cal_msd.sh复制到这个目录下，然后修改它的参数，将

里面的num_parts改为25，然后将定义输出文件保存目录的参数dir_name改为1test，这里也要注意sh文件里面执行gmx msd指令后面EOF里的内容，里面的数字是否对应了你想研究的体系组的编号；然后执行以下指令：

mkdir 1test
sh cal_msd.sh

运行之后，再将刚刚我们写好的error_cal.py文件复制到1test目录下，运行该python文件。这个时候就会直接输出扩散系数的计算结果以及误差：

平均扩散系数为：59.33183333333334
标准误差为：+/- 1.1280807319825878
hello world

然后可以再用刚刚写好的gnuplot的代码绘图看看msd曲线是否正常，一般来说误差这么小，曲线都不会有啥大问题，我绘制的图片如下：

可以看到关联时间太长的时候误差比较大，但是关联时间控制在100ps内的时候结果就比较合理。

总结

整个计算下来还是挺复杂的，计算msd并没有像gmx msd指令那样简单使用的，尤其是对于我这种多相体系的拟合，很容易得到一个特别奇怪的msd曲线，而且直接将整个轨迹投入计算扩散系数的时候会导致误差特别的大，因此这样的分割处理，选定合适的关联时间往往能够获得更加可靠的计算结果，而且这里面的操作空间很大，我们可以根据自己的体系再去调整轨迹的分割以及计算扩散系数的时间点，只要肯花时间，就能够获得很精确的计算结果。