正极材料的DFT计算
正极材料的DFT计算与思考
前段时间跟师兄合作的工作终于基本结束了,我负责了文章的计算部分,也算是我第一次完成一个成体系的计算工作,趁着现在还有点空闲时间,我想先把在之前工作的一些心得、问题以及思考记录下来。
引言
现在新能源的火爆不必多说,对于电池材料的研发一直都是一大热门,而作为电池中质量占比最大的正极材料,如何有效的提升正极材料的比容量以及循环稳定性是一个非常有意义的课题,此外,目前正极材料一般还是以金属氧化物作为基础,碍于保密原因,课题的细节我就不多赘述,金属氧化物有许多的特点,其一就是普遍具有周期性结构,建模这一块是比较好表示的,但是又由于存在离子的嵌脱,想要准确的描述离子在晶体结构中的迁移问题,又是一个非常麻烦且计算昂贵的工作,这次跟师兄合作还是以实验为主,所以计算上也是有所简化的,模型其实不算太准确。
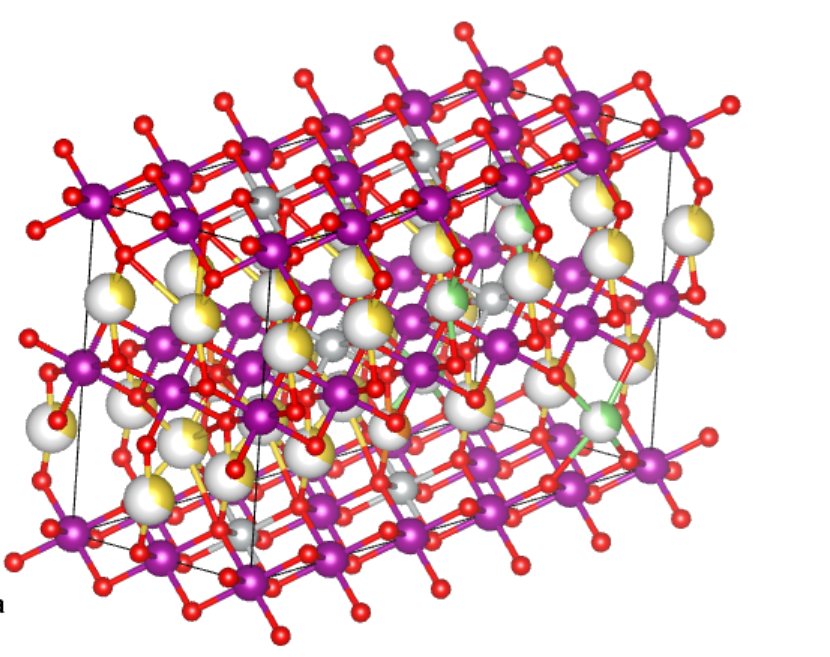
材料的容量问题其实很难通过理论去描述,在理论层面,你可供移动的离子愈多,那自然容量就高,而且对于层状氧化物,你将离子层的原子全部拿掉,也基本不会影响整个晶体模型的稳定性,计算的时候依然能够收敛(甚至于收敛速度还相当的快速),但是在实验中我们可以知道,对于电极材料的荷电状态(State of Charge),是有一个极限的,其对应着一个元素的比例,也可以理解为这个状态下的化学式,所以我们只能通过实验的值来变相的获得其在计算中可以达到的容量,从而进一步计算电极材料的其他性质。
♾️此外DFT计算也可以帮助我们去分析电极材料中电池的元素分布情况,毕竟有些时候你往电极材料中掺杂一些奇奇怪怪的金属元素,后面XRD拍出来是掺进去了,你也很难知道它能到哪一层中去了;同时,进行一些诸如neb计算的话还可以辅助分析电极材料倍率好坏的原因。
工作回顾
回顾一下自己的工作内容,其实可以分为几个部分:
- 计算掺杂元素更有可能分布在哪一层
- 计算掺杂与否是否会导致离子的积聚
- 计算掺杂是否会改善电极材料的循环性能(体积应变更小)
这些计算内容其实都是实验者,也就是我师兄在做实验以及看文献中,根据自己的体系想出来的,也就是文章的亮点(不得不佩服他的想法),当然中间也有我帮助他,告诉他那些是可以通过计算得到的,比如前两个需求,就可以通过计算能量的方法比较简单的得到对比结果。
元素的分布问题
元素的分布涉及到形成能的计算,在固相合成正极材料中,是通过将原料在球磨后直接高温煅烧的方法来制备电极材料的,这个高温过程中,随着能量的传导,晶体也随着变化,自然一般来说,放出能量越多,或者吸收能量越少的晶体构型就是成型概率更大的结构。这里我们就是通过粗略的计算其形成能来大致判断元素在哪一层的分布可能性更大。
这里一个简单的方法就是选择一个基底模型,这里我是以精修得到的模型,删去层间的阳离子(因为精修的模型其实也不是准确的,层间的阳离子占位根本不准确),随后直接用不含阳离子的层状氧化物进行计算,这里得到模型A,然后将掺杂的原子分别放在过渡金属层以及离子层,分别进行计算,最后再通过Materials Project网站获取掺杂元素的单原子能量(这里也可以自己进行计算,但是其实计算结果差异不大),再加减算一下,就可以得到其能量。
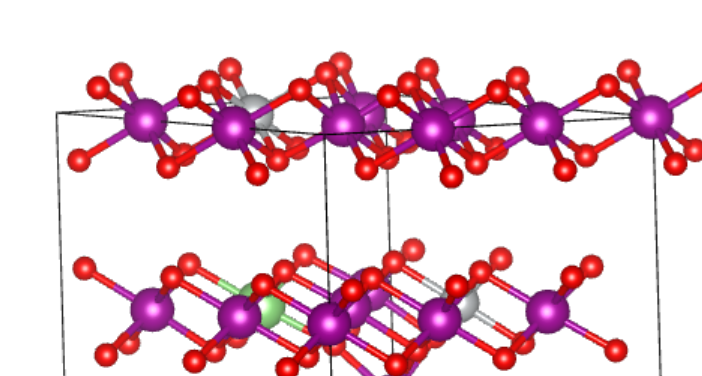
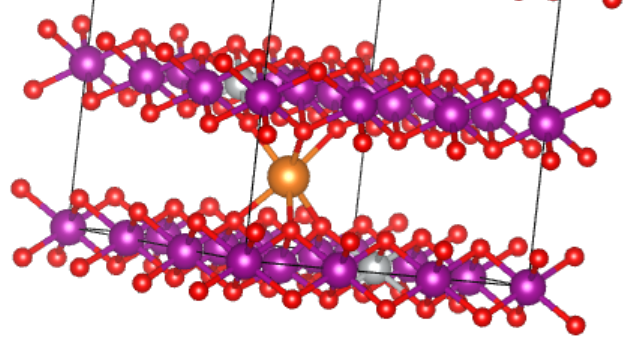
具体的计算其实就很简单了,建好模型,再对模型进行结构优化,收敛之后数据稍微处理一下就可以了,总体而言这部分工作更像是一个练手的工作,与其它文献的计算结果也基本一致。
离子的积聚
其实正极材料,我做了这些计算后感觉有一个难点就是,离子在层间的位置真的时太不好确定了,而且在实际的应用中更甚,离子会有一个迁移的过程,所以更不好确定其位置,我们也很难去确定离子会更容易堆积在哪些区域,这其中,过渡金属层又是否会对它的堆积造成影响,这也是我们这一部分工作需要探讨的。
这部分的工作我们也将它简化成为了一个能量的对比问题,还是按照能量最低概率最大的原理,我们在掺杂在过渡金属层的原子附近人为的摆放了一些原子,然后计算这个前后的能量差异,然后对比它本身在体相中堆积时的能量变化,最后来判断我们所掺杂的原子是否能够起到一个抑制堆积的效果,因为离子的堆积很明显会导致晶体内部的结构失调,从而引起体积的剧烈变化,这个是我们不想看到的。
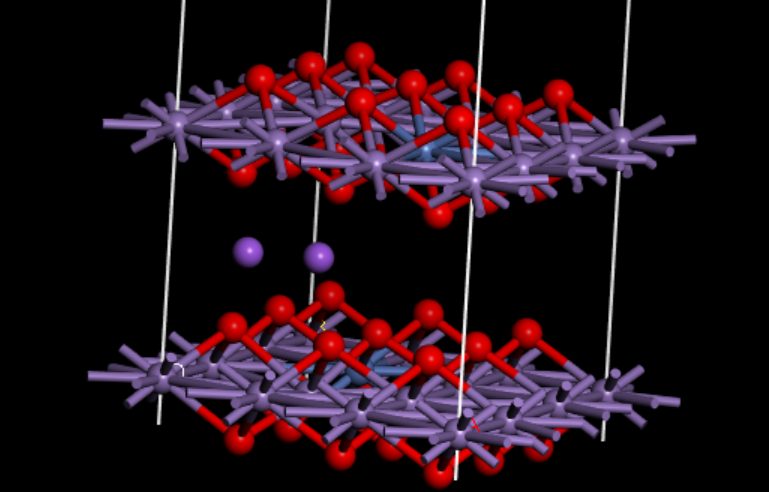
其实开始的能量部分有了上一步工作,这里做起来已经如鱼得水了,给我造成了一定麻烦的也就是离子它并不会老实的呆在你给它摆放的位置(也说明了它自己会向能量更低的点滑移),后面实际上还是有点难以界定的,不过咱们可以多做一些点位的计算,这样结果也算是可以供给参考的了。
写文章,自然不是给出一个结果就够了,还需要分析为什么,这里为了简单凝练,就用了Bader Charge来分析离子的积聚以及分散。具体的分析步骤就不多做赘述,这里将当时画的草图贴出来吧,这里有许多不足的地方,后面做了很多修改,文章中的图也没有用这个,但是其实还是可以看出掺杂与否对电荷的转移还是有比较明显的影响的。
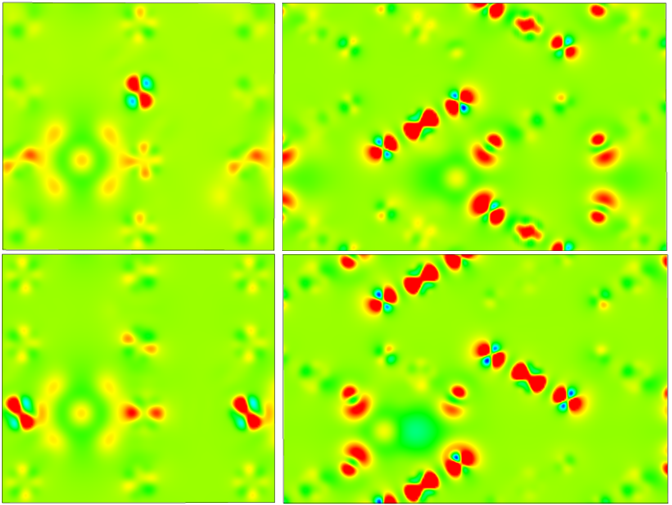
体积应变
体积应变原本以为不会是一个比较难处理的内容,但是真的计算起来却发现难度还是有的,而且最麻烦的点是,在实验中,通过原位XRD表征,我们可以直接获得实验测定的体积变化值,这对理论计算来说,想要通过计算来契合实验的值,的确是一个不小的挑战。
体积应变的计算思路其实也很简单,通过vasp的计算我们可以直接在最后导出晶胞的体积大小(ISIF=3),所以我们只需要注重模型的准确程度就行,这里我们采用了之前的探讨过的,根据电极材料的荷电状态来确定其所含的离子数目,也就是说,充满电的状态下,离子脱出,但是还是会有一部分离子留在晶体内部,而放完电之后,离子全不嵌入,也就是在实验时合成所制备晶体的离子数目,这样就算是构建了一个相对准确描述充放电之后电极材料状态的模型。随后分别计算这两个的体积变化,并跟实验值对比。
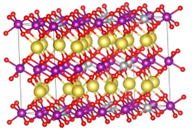
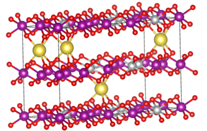
这个计算的过程也算是一波三折,修修补补,最终还是获得了一个跟实验值相吻合的结果,后面我们也对此进行了进一步的ELF分析,这次的结果分析效果也更加显著,可以很明显的看出来差异。